The classic example of the use of backtracking is in the n-Queens problem. The goal in this problem is to position n queens on an n×n chessboard so that no two queens threaten each other; that is, no two queens may be in the same row, column, or diagonal. The n-Queens problem is a generalization of its instance when n = 8, which is the instance using a standard chessboard. For the sake of brevity, we will illustrate backtracking using the instance when n = 4.

The backtracking technique with the instance of the n-Queens problem when n = 4. Our task is to position four queens on a 4 x 4 chessboard so that no two queens threaten each other. In other words, No two queens can be in the same row. The instance can then be solved by assigning each queen a different row and checking which column combinations yield solutions. Because each queen can be placed in one of four columns, there are 4 x 4 x 4 x 4 = 256 candidate solutions.

The sequence in this problem is the n positions in which the queens are placed, the set for each choice is the $n^2$ possible positions on the chessboard, and the criterion is that no two queens can threaten each other.

n-퀸 문제는 n개의 퀸을 서로 상대방을 잡아먹지 않도록 체스판에 배치하는 것이다. 즉, 두 개의 퀸이 같은 행, 열, 또는 대각선상에 위치할 수 없다. 원래의 문제는 8개의 퀸을 표준 체스판(8 x 8)에 배치하는 거지만,설명의 간결함을 위해 n=4인 인스턴스에 대해 백트래킹을 설명할 것이다. n=4일 때 각 퀸은 4개의 열 중 하나에 배치될 수 있기 때문에 4 x ​​4 x 4 x 4 = 256 개의 해답후보가 존재한다.

n-퀸 문제에서 순서(sequence)는 퀸을 두는 n개의 위치가 되고, 각 선택의 집합(set for each choice)은 체스판에 말을 둘 수 있는 $n^2$개의 위치들이며, 기준(criterion)은 두 퀸이 서로 잡아먹히지 말아야 한다는 것이다.

Backtracking is the procedure whereby, after determining that a node can lead to nothing but dead ends, we go back (“backtrack”) to the node’s parent and proceed with the search on the next child. We call a node nonpromising if when visiting the node we determine that it cannot possibly lead to a solution. Otherwise, we call it promising. To summarize, backtracking consists of doing a depth-first search of a state space tree, checking whether each node is promising, and, if it is nonpromising, backtracking to the node’s parent. This is called pruning the state space tree, and the subtree consisting of the visited nodes is called the pruned state space tree.

n-퀸 문제의 백트래킹 기법은 상태공간트리를 깊이우선탐색하여 각 노드가 유망한지를 검사하고, 만약 유망하지 않으면 탐색을 중단하고 그 노드의 부모노드로 돌아가 다음 자식노드의 검색을 계속하는 절차이다.

상태공간트리(state space tree)의 루트노드에서 잎노드까지의 경로가 해답후보이다. 만약 해당 노드의 자식 노드에서 답이 나올 가능성이 있으면 유망하다(promising)라고 한다. 반대로 노드를 방문할 때 해답이 될 가능성이 없다고 결정되면 그 노드를 유명하지 않다(nonpromising)라고 한다. 유망하지 않은 노드를 방문한 경우 부모노드로 백트래킹 한다. 이 절차를 상태공간트리의 가지치기(pruning)라고 한다.

Example we use backtracking to solve the instance of the n-Queens problem when n = 4.

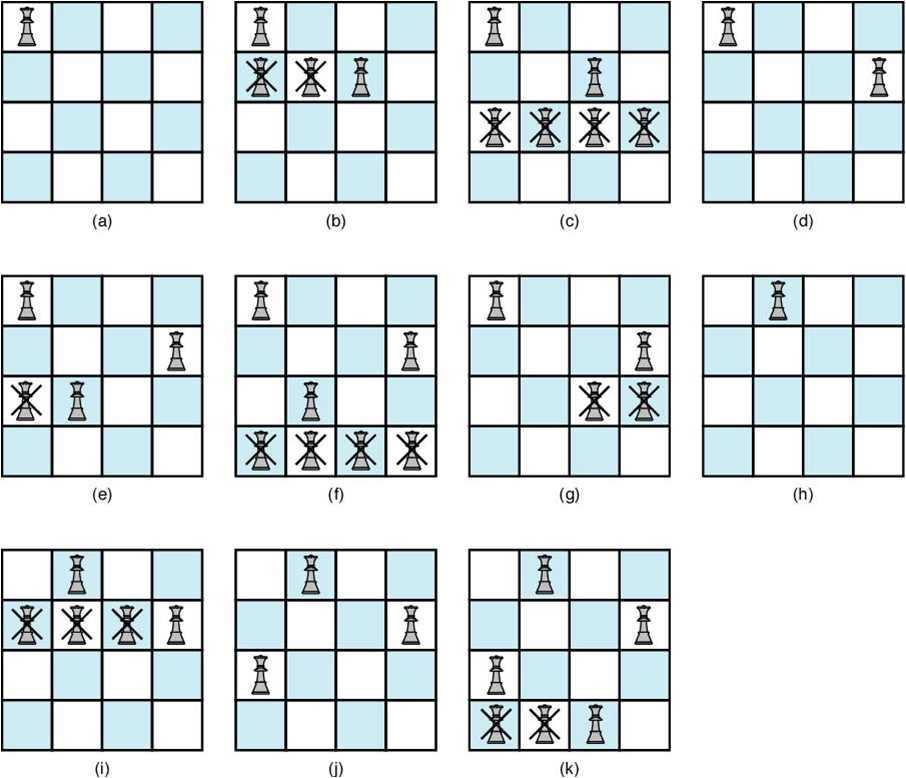
Step (a)

Step (b)

Step (c)

Step (d)

Step (e)

Step (f)

Step (g)

Step (h)

Step (i)

Step (j)

Step (k)

The Backtracking Algorithm for the n-Queens Problem

Algorithm Design

If we let $col(i)$ be the column where the queen in the ith row is located, then to check whether the queen in the kth row is in the same column, we need to check whether
$$ col(i) = col(k) $$

col(i)는 n X n 체스판의 i행에서 퀸이 놓여있는 열의 인덱스이다. col(i) = col(k)이므로 i행과 k행에 있는 두 퀸이 같은 열에 있는지 검사하는 등식이다.

Next let’s see how to check the diagonals. The queen in row 6 is being threatened in its left diagonal by the queen in row 3, and in its right diagonal by the queen in row 2. For the queen threatening from the left, the difference in the columns is the same as the difference in the rows. For the queen threatening from the right, the difference in the columns is the negative of the difference in the rows.

$$
\begin{align}
&col(6) - col(3) = 4 - 1 = 3 = 6 - 3 \\
&col(6) - col(2) = 4 - 8 = -4 = 2 - 6
\end{align}
$$

6행의 퀸은 3행의 퀸에 의해 왼쪽 대각선으로 위협받고 있으며, 2행에 놓인 퀸에 의해 오른쪽 대각선으로도 위협받고 있다.

왼쪽 대각선에서 위협하는 퀸에 대해서는 열에서의 차이(4-1=3)가 행에서의 차이(6-3=3)와 같다. 오른쪽 대각선에서 위협하는 퀸에 대해서는 열에서의 차이(4-8=-4)가 행에서의 차이(2-6=-4)의 음과 같다.

These are examples of the general result that if the queen in the kth row threatens the queen in the ith row along one of its diagonals, then

$$ col(i) - col(k) = i -k \quad \text{or} \quad col(i) - col(k) = k - i$$

일반화하면 k행에 위치한 퀸이 i행에 놓인 퀸에 의해 어느 한쪽 대각선으로 위협받고 있으면 위의 등식이 성립한다.

Pseudo Code

void queens(index i)
{
  index j;

  if (promising(i))
    if (i == n)
      cout << col[1] through col[n];
    else
      for (j = 1; j <= n; j++) {  // See if queen in
        col[i+1] = j;             // (i+1)st row can be
        queens(i+1);              // positioned in each of
      }                           // the n columns.
}

bool promising(index i)
{
  index k;
  bool switch;

  k = 1;
  switch = true;                  // Check if any queen threatens
  while (k < i && switch) {       // queen in the ith row.
    if (col[i] == col[k] || abs(col[i] - col[k]) == i - k)
      switch = false;
    k++;
  }
  return switch;
}

Source Code

// File: nqueens.h
#ifndef NQUEENS_H
#define NQUEENS_H

namespace algorithms
{
  void queens(int i, int n, int* col);
  // Problem: Position n queens on a chessboard so that no two are in the same
  // row, column, or diagonal.
  // Inputs: positive integer n, an array of integers col indexed from 1 to n.
  // Outputs: all possible ways n queens can be placed on an n x n chessboard so
  // that no two queens threaten each other. Each output consists of an array of
  // integers col indexed from 1 to n, where col[i] is the column where the queen
  // in the ith row is placed.

  bool promising(int i, int* col);

  template <typename Item>
  Item* get_vector_space(const int n)
  // Prostcondition: Return the array containing n spaces
  {
    Item* v = new Item[n];
    return (v-1); // offset the pointer
  }
}

#endif

// File: nqueens.cpp
#include <iostream>
#include <iomanip> // Provides setw
#include "nqueens.h"
using namespace std;

namespace algorithms
{    
  void queens(int i, int n, int* col)
  {
    int j;

    if (promising(i, col))
    {
      if (i == n)
      {
        // Print col[1] through col[n]
        for (j = 1; j <= n; ++j) // Print index
          cout << setw(7) << "col[" << j << "] = " << setw(2) << col[j];
        cout << endl;
      }
      else
      {
        // See if queen in (i+1)st row can be positioned in each of the n columns.
        for (j = 1; j <= n; ++j)
        {
          col[i+1] = j;
          queens(i+1, n, col);
        }
      }
    }
  }

  bool promising(int i, int* col)
  {
    int k;
    bool is_switch;

    k = 1;
    is_switch = true;

    // Check if any queen threatens queen in the ith row.
    while (k < i && is_switch)
    {

      if (col[i] == col[k] || abs(col[i] - col[k]) == i - k)
        is_switch = false;

      k++;
    }

    return is_switch;
  }
 }

// File: nqueenstest.cpp
#include <iostream>
#include <cstdlib> // Provides EXIT_SUCCESS
#include "nqueens.h"
using namespace algorithms;

int main( )
{
   // if n = 8 and  there are  8 x 8 chessboard
  const int N_QUEENS_SIZE = 4;
  int* col = get_vector_space<int>(N_QUEENS_SIZE);

  queens(0, N_QUEENS_SIZE, col);

  delete [ ] (col+1);
  return EXIT_SUCCESS;
}

Time Complexity Analysis

Worst-Case Time Complexity

• $O(n) = 1 + n + n^2 + n^3 + … + n^n = \frac{n^{n+1} - 1}{n-1} \in \Theta(n^n)$

It is difficult to analyze n-Queens Algorithm theoretically. To do this, we have to determine the number of nodes checked as a function of n, the number of queens.

Algorithm 1 We can get an upper bound on the number of nodes in the pruned state space tree by counting the number of nodes in the entire state space tree. This latter tree contains 1 node at level 0, $n$ nodes at level 1, $n^2$ nodes at level 2, …, and $n^n$ nodes at level n.

$$
\text{The total number of nodes is}=1 + n + n^2 + n^3 + … + n^n = \frac{n^{n+1} - 1}{n-1}
$$

This analysis is of limited value because the whole purpose of backtracking is to avoid checking many of these nodes.

가지 친 상태공간트리에서 전체 노드의 수를 세어 노드 개수의 상한을 구한다. 하지만 이 분석은 의미가 없다. 상한값으로는 백트래킹을 통해 점검하는 노드의 수를 얼마나 줄였는지 알 수 없기 때문이다.

Algorithm 2 Once the first queen is positioned, the second can be positioned in at most seven columns; once the second is positioned, the third can be positioned in at most six columns; and so on. Therefore, there are at most
$$
\text{Promising nodes}= 1 + n + n(n-1) + n(n-1)(n-2) + \cdots + n!
$$

두개의 퀸이 같은 열에 위치할 수 없다는 사실을 이용하여 유망한 노드를 센다. 그러나 이 경우에도 알고리즘의 복잡도를 정확히 산출하진 못한다. 왜냐하면 대각선 점검을 고려하지 않았고 유망한 노드와 유망하지 않은 노드 둘다 포함하고 있기 때문이다.

Backtracking A straightforward way to determine the efficiency of the algorithm is to actually run the algorithm on a computer and count how many nodes are checked.

위의 분석(Algorithm1, Algorithm2)으로는 백트래킹 알고리즘의 효율성을 제대로 파악할 수 없다. 유망한 노드의 개수를 정확하게 구하기 위한 유일한 방법은 실제로 알고리즘을 수행하여 구축된 상태공간트리의 노드의 개수를 세어 보는 것이다.

However, running an algorithm to determine its efficiency is not really an analysis. We did this to illustrate how much time backtracking can save. The purpose of an analysis is to determine ahead of time whether an algorithm is efficient.

In the next section we show how the Monte Carlo technique can be used to estimate the efficiency of a backtracking algorithm.

하지만 이 방법은 진정한 분석이 아니다. 분석은 알고리즘을 실제로 수행하지 않고 이루어져야 하기 때문이다. 위의 표는 백트래킹으로 n-퀸 문제를 해결하면 얼마나 시간을 절약할 수 있는지 설명하기 위해 알고리즘을 실행한 것일 뿐이다. n이 커질수록 상당한 시간 절약이 가능하다.

몬테 카를로 기법을 사용하면 백트래킹 알고리즘의 효율 추정이 가능하다.